As part of my interest for Vector Graphics technologies, I had look at the Freeform Vector Graphics (FVG) technology proposed by Microsoft Research. After all, it differs from SVG only by one letter.

The paper describing the technology is available here. A video presenting the approach is also provided by the authors here. The approach is in general an extension or alternative to the work on Diffusion Curves. It enables the control of the interpolation of colors between diffusion curves (or points), with a higher order of smoothness if necessary.

This post reports on my understanding of the method and of its implementation, focusing on the use of the software and on some aspects not dealt with in the paper and is intended for people who have already a good understanding of the paper. If you notice any mistake, if it is unclear or if you disagree, please leave a comment.

Installation

I started by downloading the software. The installation of the software on my laptop (Win 7 pro, 64 bits) went well but the software was simply not running, and did not display any error message. Thanks to Mark Finch (the main author), I saw that the system log indicated an error of type 0xE0434352 in KernelBase.dll. Trying on my desktop, I had more visible/useful error messages such as System.IO.FileNotFoundException and  System.FormatException. The last one led me to changing the regional settings to English as described here. And then, it worked, even on my laptop.

Software overview

Once the software starts, it shows the following screen. The controls to author an FVG image are provided on the left and at the top. The real-time result of the authoring is given in the bottom right part.

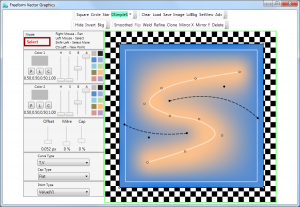
The controls allow you, among other actions, to add new or modify existing points or curves, to set/modify the color, to zoom or pan on the image, etc.

One remarkable aspect that I discovered using  the software and that is not mentioned in the  paper is the color space. The software uses the HSBA space, whereas the paper only talks about 4 channels, without mentioning if it is RGBA, sRGBA, or others.

A dropdown list proposes to select the curve type among the basic types: Value, Tear, Curve, Slope and Isogram; or among many more complex types. Not that the type “Isogram” is called in the paper “Contour” (with the same meaning according to Wikipedia).

Note also that the list distinguishes the Core types from the Extended types but apparently some Compound Curves (as defined in the paper) are also part of the Core types, such as “VS” (Value-Slope), “VC” (Value-Crease), or “T,V” (Tear, offset, Value).  I can’t see why “VS” would be more a Core type than “VT”, but that’s not really important.

Also the Null type is an extended type and is abbreviated with the letter N, which is a bit confusing as the paper uses N for Contour (Isogram). The Null curve does not seem to have any effect on the rendering. For instance, it is unclear why a “V,N,V” curve is not replaced by a “V,V”.

 

We can also see from this list (and from the user interface of the software) that only 2 colors can be used in a compound curve, which is similar to the orginal diffusion curves (color on the left, color on the right) but I believe that this is restriction of the software, the paper does not mention this restriction.

Here is a review of the core curve types:

• “VS” is simply a Slope curve (zero derivative across the curve) with explicitly assigned color(s) along the stroke.
• “VC” is simply a Crease curve (color continuity, but no smoothness across the curve) to which color(s) is(are) assigned along the crease.
• “T,V” is a Tear curve (color discontinuity) and a Value curve (color(s) along the curve) on its right, separated by a user-specified offset.
• “T,V,T” produces a stroke along the curve with a width equal to two user-specified offsets and with color(s) along the stroke.
• “V2C,V1,V2C” specifies 2 crease curves, whose colors are specified to be the same, with an additional (smooth) curve in between. The images below shows an example, where the curve is a straight vertical line segment, and the associated color profile across that curve (image underneath).
  Note that even if the same colors (V2) are specified on both sides of the compound curve, because of other features in the image, the final colors on both sides of the curve may be different. In this particular example, however, the non-symmetry of the result is unexpected. This may be due to the fact that the curve is not centered in the image and to the boundary conditions, but moving the curve does not seem to help.

• “V2S,V1,V2S” is similar and produces two zero-cross-derivative smooth curves with the same color, with a smooth color transition to a different color in between, as shown in the images below. The color profile along a horizontal line is also shown underneath.

• “V1,T,V2” is a classic diffusion curve, with two different colors torn apart by a tear curve (see images below), with the difference that some explicit offset between the two colors is specified. In the software, the minimum offset is 0.51 pixel, which makes that minimum distance between color 1 and 2 is more than 1 pixel. This is probably to avoid having two colors conflict at a given pixel.

• “V1S,T,V2S” is similar with the additional constraint that the derivative is zero before and after the tear curve (see image below). This can be seen in the color profile.

 

The list of extended types for compound curves is very long and I won’t detail all of them here. I’ll let you experiment with it if you want.

The software gives another list to set the type of a feature point, with 5 values: Null, Value, Critical, CriticalValue, Crease and CreaseValue. The published paper only talks about the Value and Critical type. One can guess that the Null type is not used during rendering, and that the CriticalValue type combines the Critical and Value type. The Crease type is probably the equivalent of a Crease curve but shrunk down to a point, i.e. that it removes the Dxx, Dyy, and Dxy penalties on the surrounding pixels, and the CreaseValue a combination of this Crease type with a Value type.

Advanced Controls

The user interface has lots of other controls, which are not intended for the end user, but where interesting things happen. The upper controls enable the author to load or save the content, to modify curves (weld, smooth), etc; but the most interesting control is the “Adv” button, which shows the following check boxes.

According to my experiments, some are not very important as they control only some elements of the UI and not the method used to produce the image. Some others are more important. I’ll present here their effects.

• “Show Wgt” brings up a set of sliders as follows:

The upper sliders seems to control the weights used to produce the image, as described in Equation 1 in the paper. However, the weights are named differently from the paper. In the paper, they are called w0, w1, w2, wp (one for value point and one for value curves), wt (one for slope and contour curves and one for crease curves). After different attempts, my understanding is that:

• RegularDiag is related to w0, the diagonal regularization term;
• RegularLap is related to w1, the weight of the Laplacian term also used for regularization;
• D2M2Weight  is related to w2, the thin-plate spline weight, which brings the high-order smoothness to the image;
• GradientWeight corresponds to wt (for slope and contour curves).
• For all the other weights, it is unclear to me, if there is a mapping to the paper’s weights.

• “Show Term” brings up another set of sliders as follows:

• “Blit Nearest” determines how the computed image is copied in the display area (the right-bottom part of the window). That area is of a fixed size: 512×512. So if the computed image size is smaller that the display area, some special blitting must be done. The “Blit Nearest” activates a nearest neighbor interpolation and one can see the aliasing artifacts as visible in the paper.
• “Laplacinate” seems to use the weights as indicated in the paper, when only the Laplace operator is used and not the Thin-Plate Spline operator. It can be used to show the result of a lower level of smoothness. The images below shows the “Flames Simple” example when this option is on and the color profile across a horizontal line going through the green feature at the bottom.

• “Use MKL” probably indicates that the Intel Math Kernel Library (as indicated in the paper) is used.
• “Fill Holes” probably activates the flood fill algorithm as presented in the paper. As an example, the image below (and its detail) show what happens when it is turned off. Some areas are simply left white.

• Unfortunately, the “Relax Final”, “Lo Res Up”, “Upsample Up”, “Smart padding”, “Big Pad”, “Fast Path”, “DynaBounds”, “Slop Bounds” options are not documented and it is not clear from the paper or from my experiments what part of the algorithm they control.
• “Hide Ctl Pts”, “Show Tears”, “Checker”, “Show Unused” controls some aspect of the display: showing control points or not, showing tear curves or not, showing a checker board in the background or not, showing points which contribute colors differently from the others (control points).
• “Save Float”, “Compare”, “Diff”, “Pan Show”, “Show 2nd” are not clear to me but I don’t think they affect the algorithm.

Rendering Quality

The rendering results provided here by the authors are quite impressive, and show that the proposed approach could be an interesting tool for graphics artists. However, I noticed a few artifacts which I think are worth mentioning.

Pixel error

In the following image (and in the following closeup), you can see that in some cases, the rendering of sharp features produces a black pixel. I think this is a problem that the pixel gets “pinched off” at the coarsest resolution when the direct solver is called. No equation except the regularization term apply to this pixel, which leads to a black pixel. This pixel cannot be ‘fixed’ by the flood fill algorithm as it is not a ‘undefined’ pixel.

 

Stability

As described in the paper, the software “uses two solution modes: a faster one used for interactions like control point dragging and image panning […], and a slower one invoked after UI button-release”. The left image below shows the rendering of the cup example during a drag operation. It should be compared with the final result (right image) and as can be seen, the image quality is poorer during the drag operation.

But another effect is noticeable during the drag operation. Some weird color artifacts appear, but they are different from frame to frame. This can be seen on this video. This seems to indicate a lack of stability of the fast rendering mode. Fortunately, these artifacts disappear when the mouse is released, as can be seen at the end of the video.

However in some cases, even after the button is released, the result is not the expected one. The following images show 3 different rendering of the flames example, with the same settings, the only difference is the position of the features. You can notice that the 3rd flame is rendered differently. I don’t have a definite explanation, but my guess is that, at this resolution, the value points located in the flames are too close to the the border and the rasterization of the features proposed in the approach has some problems.

Image borders and boundary conditions

The paper indicates that the “goal is to support a virtual canvas of infinite extent” and that a window which contains all the features “applies ‘natural’ boundary conditions, equivalent to a tear curve circumbscribing the entire boundary”. I noticed some strange artifacts of this approach, as depicted in the following images. The right most flame at the image border shows a different color depending on how much of the flame is in the image. It gets more yellow or more red/orange.